前回まで─
三角関数（三角比）というと、「主に電磁気学などの物理分野で使うから必要」というような一般論がありますよね。確かに実生活に役立つような段階となれば、その通りです。
確かに数学という枠の中だけで考えれば、三角比の相互関係や三角関数そのものを深めていく目的は分かりにくいし、どうしても道具としての意味合いが強いことは否めない（汗）。
「本当の使い勝手は物理を学んで初めて分かる」と仰る諸先輩方の意見ももっともかもしれませんね。
でも、それとは切り離して考えてみてもなお、‘三角関数を学ぶ意義’というのはあると私は思うのです。
その発想がむしろ数学的
いったん話題を変えましょう。
私たちは普段、数字が10ごとに繰り上がる「10進法」を使っています。大きな数も小さな数も基本的にはこの表記法によって大小を解釈しています。
ただ、この表記法では正確に表せない‘量’というものもありますよね。
そうです、「1÷3＝0.333…」みたいな場合です。
なんだ、そんなの分数で「
」と表せば解決じゃん！ ─まったくその通り。
ここで「そんなのアリ？反則でしょ～」という声は聞こえてきません。分数もまた、私たちが慣れ親しんだ‘量を表す表記法’だからです。
では、次の場合はどうでしょう。
「円周率は約3.14なんだけど、これじゃあ少し不正確だよね」
「それなら3.141592にしようか」
「さっきよりマシだけど、それでもまだ正確とは言えないね」
「だったら、もういっそのこと‘π’ってことで！」
「え？どういうこと？」
「πという記号を、円周率という無限に続く小数を表すことにしようってこと」
小学生にこういう話をすると、「そんなんでいいの！？」という意見が出たりします。
いいんです、そうと決めてしまえば。
そもそも私たちに染みついているあらゆる概念は、何かしらの‘決め事’から出発したものばかりなのですから。
でも冷静に考えてみて下さい。これはすごいことですよ！
円周率のように小数でも分数でも正確には表せない無限に続く数（無理数いいます）を「文字」という有限の入れ物に詰め込むという暴挙（笑）に出て、挙句その値を正確無比なものとして扱うことを成功させてしまったんですから。
他に無理数と言えば…例えば「2乗したら3になる数」なんていうのがありましたね。これも「1.7320508…（人並みにおごれや…というゴロ合わせがありますね）」と無限に続き、正確には表せません。だから「
」という記号を生み出して、「これで正確無比な値を表すものとする～！」と決めたわけです。
話をもとに戻します。三角比の件でした。
三角比に関しては、今挙げたような例とは実情が多少違いますが、やはり「正確に表せないものを表現する新概念」という意味では同じです。
そう考えると、これは工学的ツールというより、むしろ数学的な発想・必要性から生まれたもの、そんなふうに私は感じて止まないのです。
あちらが立てば、こちらが立たず
もういい加減に具体的な話をします。
三角比といえば角度（よくθと表す）がつきもの。
ただ、この開き具合を表す‘角度’ってやつが意外にクセモノなんですよ。
まず、開き具合の区切りである一周というやつを「360」という数で表しています。
これは古代のバビロニアやギリシャで、夜空の星が約360日で同じポジションに戻ってくる─つまりそれを一年とした─ことが影響しているとのこと。
今でもそれを採用し続けているのは、360が比較的多くの約数を持っていて使いやすいという背景があるわけで、このこと自体はやっかいというわけではありません。むしろ一周の角度をキリよく100なんかにするよりはずっと賢い選択です。
じゃあ何がやっかいなのか。
一言で言うなら、「角度の世界は長さの世界と相性が悪すぎる」ということに尽きます。
具体的に見てみましょうか。
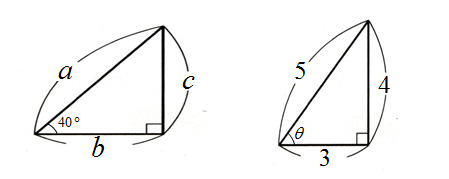
例えば次のような直角三角形です。
（※三角形は最も単純な図形であり、中でも直角三角形はピタゴラスの定理より、２辺の長さが決まれば自動的に残りの長さも決まるので、例として最適なのです）
左の三角形は、角度θの部分が40°だとわかっています。もちろん残りの角度は50°になりますから、三角形の形は特定のものに決まります。違う形にはなり得ません。
当然この三角形の3辺の長さの比も、ある決まった比になる。そこで例えば「a：b」はいくらになるのか？
結論から言います。「約1：0.766」です。
ん？何ですか、その‘約’っていう枕詞は。。。
はい、これはですね。「三角比の表」というものがありまして、そこには1°きざみで直角三角形の辺の比の近似値（近い値）が載っていて、そこから引っ張ってきた値なのであります。
「でもさあ、もう√とかも使いこなせるんだし、正確無比な比で表せばイイじゃん」
そう思った人、実に申し訳ないです。
こればっかりは無理なんです。この三角形には、この三角形にしかない固有の辺の比というものが明らかにありながら、私たちが知っている「量を表す手段」ではどうにも表現できないんです。
とりあえずそれは置いといて…。
今度は右の三角形を見てください。これは皆さんご存知（とは限らないですが…）有名な直角三角形で、ちょうど3つの辺の比を整数だけで表すことの出来る珍しいパターンです。
で、この三角形の角度θは何度でしょう？
結論を言いますよ？「約53°」となります。
え～…またまた‘約’ですかぁ？
はいスミマセン、これも正確無比に表すことは不可能なんです。
これはどういうことかと言うとですね、角度を表す世界と長さを表す世界とでは、「最初から別のものさしを使って大きさを考えている」ということなんです。
ふってある数字は同じ10進法でも、メモリの間隔やふり方はまるで違う──まさに定規と分度器の違いそのものです。
なので、角度から形を決定すると長さが正確に表現できないし、長さから形を決定すると角度の正確性が甘くなる。
あちらが立てば、こちらが立たず…ただ一つの答えがあるはずなのに、それを言い表す言葉が無い。非常にもどかしい状況となるわけです。
ちなみに…
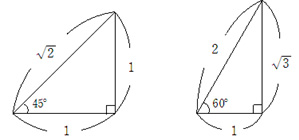
無数とも言える事例の中で、ほんの一握りの「あちらもこちらも立っている」ケースがあります。下の２つはその中でも有名な三角形です。
中学生のときに覚えましたよね～。
「1：1：
」「1：2：」と、何度も口ずさんだに違いありません。
左は正方形の半分、右は正三角形の半分、ということで、図形的な性質から角度と長さの関係を正確に表現できているレアなケースです。
（※一応上記以外にも、角度θが3の倍数であれば、理論上は辺の比を正確に表すことができます。でも、そのほとんどが複雑で長ったらしい値になるのと、角度θがそれ以外の数値なら、結局は長さの比は正確には表せないのです）
橋渡しをするということ
長さと角度。基本的に歩み寄ることのない両者を放っておくことも出来ます。
しかしそれでよいのでしょうか。
答えは否。
数学者たちの探究心が、世界の違う両者をつなぐ架け橋を少しずつ築いていったのです。
それが三角比。
お得意の「決め事」をつくるわけです。
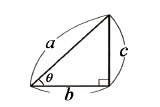
どんな決め事か──図の状況での長さaから見た長さbの倍率、すなわち
を、θを使って表現できれば…ということで形になったのが「
」
これで辺の比と角度θをミックスして、とりあえず‘関係を表す式’になったぞ、と。
つまりですね、さっきまでは「角度θが40°のの直角三角形」において、辺の比である「a：b」を正確に表す言葉を持たなかったけれど、今は「辺bは辺aの何倍か」を正確無比に表す表現法を手に入れたと言えるのです。
それが「
」
そのおおよその値は0.766で、正確無比な値は──ひとまずそう表現すると決めたということです。
じゃあ「辺の比が3：4：5の直角三角形の角度θは？」
うん、イイ質問ですね。
「
を満たすθ」ということになります。
この三角比の基礎概念は、すでに紀元前からあったというのですから驚きです。
なんかだまされた気分ですか？
そう、ある意味だましているのかもしれません。
しかし、数学の面白いところは、ひとまず自分をだますところにあるといってもよいのではないでしょうか。
だって、文章題を解くときに「わからない部分をxと置いて…」ってやってるでしょ？それって、未知の値を‘ひとまずわかったものとして’式に組み入れているわけじゃないですか。
その行為はまさしく、意図的に「自分をだましている」ことに他ならない。
そして人間の素晴らしいところは、自分を軽くだましながら、それがどんなものに応用できるかという損得勘定を抜きにして、純粋にその‘決め事’をスタートとして閉じた世界の中のルールを構築しようとする探究心。
数学の素晴らしいところは、必ずその期待に応えてくれるような美しい法則を用意しているということ。
など、信じがたいほどの美しい結論を見せてくれます（これらを導くのはかなり難しいけれど、結果としてスゴイことがわかる！ということだけは理解しておきたい）。
その上、自然界とりわけ物理法則を記述するための絶大なツールになるというのですから、これはもう三角比・三角関数の入り口ぐらいには立っておかないと、人生損をするというものです。
以上、長文失礼いたしました。読んでくれた方、ありがとうございました。
ふぅ…とりあえず来週は日記でイイですか？（笑）
面白い記事でした。
ありがとうございました。