図形の面積は？
今回は私が考えた軽めの平面図形問題を紹介します。
一応どの年代の子にもチャレンジしてもらえる内容ですので、やってみて下さい。
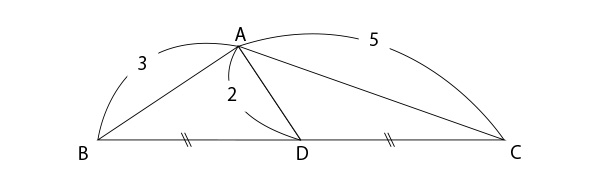
図のように三角形ABCの辺BCに中点Dをとります。AB＝3cm，AD＝2cm，AC＝5cmで、BD＝DCです。このとき、三角形ABCの面積を求めなさい。
実はこの問題、色々な解法があります。
一つは中学生向けに「三平方の定理」を使った解法。ただし、これは補助線や立式が非常に複雑になるのであっさり解きたい人には不向きです。
まだ高校生向けの「三角比の余弦定理」の方がシンプルです。
ちなみにこの解法に関しては参考までに最後に紹介します。
ということで、メインとしては小学生でも取り組める方法で解説します。
切ってつなげる解法
さて、これは本当にあっさりした解法です。
まず、BDとDCの長さが同じだということに注目します。
そして三角形ADCを、点Dを中心として180°回転させBDとDCをくっつけます。
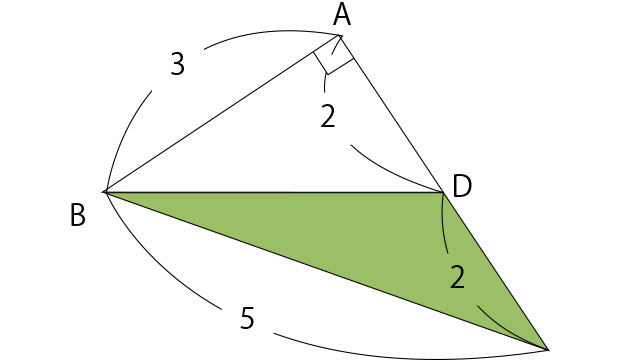
するとどうでしょう。
これ、前々回のブログ（2015年5月27日「質問にお答えします～小学生でもわかる数学とは？～」）でちょっと紹介した「3：4：5の直角三角形」ではありませんか！
三辺がこのような比の三角形は3と4の間の角が直角になることが分かっていますので、まさにこの直角三角形の面積そのものが、本問の正解となります。
答え 6cm2
2023年4月16日㈰親学無料セミナー開催‼
毎回ご好評をいただいているセミナー親学ですが、今年は“子どもを伸ばす親のあり方を多角的に考える”をテーマに皆様と一緒に考えていきたいと思います。
2023年4月16日㈰ の親学無料セミナーでは
「子どもを”活躍する人間”に育てたい ～カギになる３つの能力をどう伸ばすか～ 」
をテーマにお話しします。
いま急速にAI化が進み社会の構造も変化しつつあります。
２０３０年以降のいまある仕事の３分の２がAIに取って替わられると予測する経済学者もいます。
ここで大事なのは機械（AI）が代替できない能力―人間にしかできない能力―をいかに身につけているかです。
今回のセミナーでは、お子さまがこの激変時代を生き抜く能力をいかに身につけるか。
親がどのように導き、この能力を育んでいくか。
社会背景を踏まえながら多角的にお話ししていこうと思います。
詳細・お申し込みはこちら
〈次回セミナーの予定〉
■５月２１日㈰ 親学無料セミナー
「父親のための１５０分」～今の時代に必要な父親像について～ ※4/1申込受付開始予定
■５月開講 母親塾HMC（有料講座） ※4/1申込受付開始予定
コメントはお気軽にどうぞ