早すぎた天才
いきなり質問です。
皆さんは、この風景を見て何を考えますか?
あ、ちなみにこれはデザイナーさんに頼んで描いてもらったイラストなので、実際はリアルな‘日没時、地平線スレスレあたりに見える太陽と半月’という風景だと思って下さい。

「キレイだなぁ」とか、
「こういう壮大な風景を見てると、自分はちっぽけだと感じるよ」など、感想は人それぞれでしょう。
ところが世の中には…、
「この状況って、自分の正面に月、月の真横に太陽があるってことだよね?」
と、通常の斜め上をいく発想をする人もいるのです。
実はこの人こそ、今回のmy偉人であるアリスタルコス。
今から2300年前、古代ギリシャの人物です。
なにが偉いって、彼こそが記録上「初めて地動説(太陽中心説)を唱えた人」なのです。
ん?地動説って、「太陽が動いているように見えるけど、実は地球の方が動いているんだよ」っていうやつだよね…それって今から500年ぐらい前の、コペルニクスとかガリレオが最初に言ったんじゃないの?
そう思った人が多いのではないでしょうか。
確かに、彼の名はあまり世間には浸透していません。
それはきっと、アリスタルコスという天才があまりにも早い時代に生まれてしまい、ガリレオたちのようにパラダイムシフト(それまで常識だと思われていた認識や思想が大きく変化すること)を起こすような一大論争にはならなかったからでしょう。
事実、彼の考えは記録には残っているものの、周囲に受け入れてもらえず、約1800年の永きにわたり忘れ去られます。
そう、コペルニクスによって彼の偉業が再発見されるまで。
コペルニクス自身、天動説に対して腑に落ちない思いを抱いていたようですが、忘れ去られたアリスタルコスの考え方に勇気をもらい、地動説を確信していったようです。
彼の科学的思考
アリスタルコスが先の風景から想像したことをもう一度言います。
「自分の正面に月、月の真横に太陽がある」でした。
これは、月がちょうど半月に見えることからの発想です。
そして、月と自分(地球)と太陽を結んでできた角度を測りました。
現代で言う分度器のようなものを使ったのか、単に開き具合をメモしたのかは分かりませんが、とにかくそのときの角度は約87°だったようです。
この状況を俯瞰的に眺めると…月・地球・太陽の三者が右図のような位置関係になるということに気づきます。
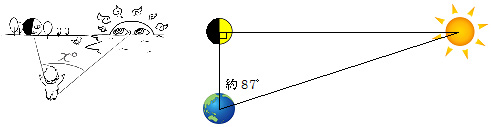
…って、ちょっと待てよ、地球?
そのような疑問を持った人、鋭いですね~。
そう、紀元前というはるか昔に、大地が球形をしていたことが分かっていたのか?
実は知られていたんです。
古代ギリシャの知識人の間では常識でした。その頃、他の地域では「海の果てには底なしの滝がある」とか「我々の大地を支えているのは象で、その象は亀や蛇の上に乗っている」などと考えられていたのに、です。
細かいことを説明していると、それだけで一つのお話になるほど長くなるので、簡潔に言いますね。
要するに古代ギリシャ人たちは、星空の見え方や、その他の身近なものごとの観察から、大地が球形をしていることを確信していたのです。さらにその周(赤道)の長さも、計算によってかなり正確に把握していました。
古代の知恵、恐るべし!ですね。
話をもとに戻します。
月・地球・太陽が先のように直角三角形を形作っていますが、角度が確定しているので、自分でそのミニチュア版を描いてみたのです。いわゆる相似な縮小図を、です。
皆さんも描いて見ればわかりますが、87°って限りなく直角に近いですよね。
だから、実際にこの直角三角形は、かなり平べったいものになります。
で、彼は描いてみた直角三角形の「一番短い辺」と「斜辺」の比、言い換えると「地球から月までの距離」と「地球から太陽までの距離」の比を、測ってみたわけです。
その結果は、約‘1:19’という比だった。
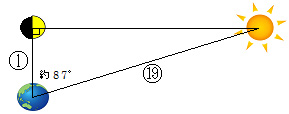
(※ちなみに、現在知られているその比は、約1:400であり、かなり見当違いなものになっている。原因の一つは「本当に87°なのか」ということ。1°違えば三角形の形にかなりの違いが生じるだろう。そして「そもそも完全な半月と言えたのか」という疑問もある。このような誤差が積み重なったと考えれる。しかし重要なのは「地球から見たら、月よりも太陽の方がずっと遠い」ということ。それを強調しておきたい)
さて、ここからですが皆さん、日食を思い出して下さい。
地球から見た月と太陽の大きさは、ほぼ同じですよね。
だから下の図のように目線のラインの中にすっぽり月も太陽も収まるはずです。
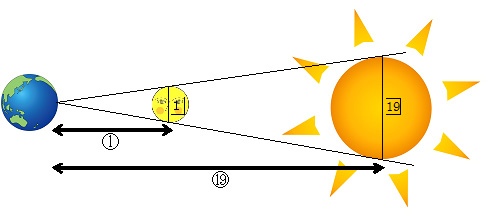
で、アリスタルコスの観測によれば、地球からの月までの距離と太陽までの距離は、1:19なのですから、直径の比も同じになっているはずだ、ということです。
(※図の中に出来た二等辺三角形は形が同じなので、小さい方から見て大きい方の高さが19倍なら底辺も19倍だという理屈)
これで、月よりも太陽が大きいことは間違いないだろうと。
さらに彼は地球との大きさの関係まで考えた。
それは月食時に月に映る地球の影から考えた(驚くことに、地球の影が月にかぶってしまうのが月食であることをギリシャ人は知っていた!)。
ざっくり言うと、彼は月食時に月に映る地球の影に注目し、カーブの曲がり具合から、地球の大きさを見積もったんですね。

こうして彼は、地球の直径は月の約3倍(本当は3.6倍ほどだが)であることを突き止めたというわけです。
さて、トータルで考えてみると、月:地球:太陽=1:3:19となるので、地球から見た太陽の大きさは6倍以上。
直径で比較してその差ですから、体積にすると3乗の216倍以上…。
ここでアリスタルコスは考えます。
「小さな物体が自分より圧倒的に大きな物体を振り回すことなどあるのだろうか?」
この問いは、赤ちゃんが横綱をブンブン振り回すことができるのか、という疑問と同じで、物理的に不自然だと誰もが経験的にわかることです。
つまり、回っているとしたら太陽ではなく、私たち地球の方に違いない─。
観測の精度という問題はあるものの、彼の思考は単なる憶測の域を超え、完全に科学的といってよい考察によるものなのです。
後に‘古代のコペルニクス’と言われるようになった彼ですが、私個人としては、もっと彼にスポットを当て賞賛してもよい人物なのではないかと思い、紹介しました。







コメントはお気軽にどうぞ