結論は出ず、だからツイートするのみ
計算上は疑いようもない、だが感覚的には受け入れがたい。
そんな切ない初冬の想い出が誰にでもあると思う。
今日はそんな私のつぶやきを聞いてほしい。
ある立体の体積を求めてみた。
どんなヤツかって?
これでっす。
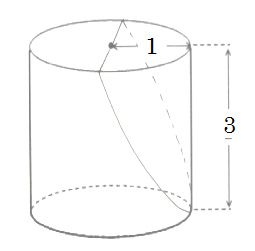
簡単に言うと、「半径1の円を底面とする高さ3の円柱」の上面の直径に包丁の刃を当あて、一気に右下までななめ切りしたときに切り取られる‘爪’のような立体(どうやら爪形と呼ぶらしいのだが)」です。
で、この爪形の体積を計算してみたところ、なんと2だったと。
ちなみに求め方は高校3年生が学ぶ「積分」というもので求め、この数値は間違いがないはずです(別々の4通りの方法で求めて全て一致したので)。
求め方そのものはここでは割愛します。
で…2点ほど現在考え中のことがあるのでつぶやきます。
①答えに「π(パイ)」すら入っていない不思議
そもそも、もとの円柱の体積が3π(パイ)です。
そりゃそうですよね。円の面積は「半径×半径×π(パイ)」ですから。π(パイ)は含まれます。
なのに切り取った爪形の体積に円周率π(パイ)は登場せず。
小学生でもわかる普通の整数…。
しかし計算は間違えていない。
それで切り方を変えてみたところ、案の定奇妙なことになりまして…。
包丁を当てた場所は上面の直径部分ですが、円の中心を通らないように少しずらした位置から切ると、なんと答えには「π(パイ)も√(ルート)も含まれるような汚い答え」になりました(汗)。直径に刃を当てて切ったときのみ、きれいな答えになるようです。
そしてなんと、かのアルキメデスが爪形の体積について言及していたのです(驚)。不完全な理論ではあるものの彼の出した結論自体は正しいようです。
現在のような使い勝手の良い積分法がなかった紀元前によくもまあ…。
②公式化する意味はあるのか?
これだけきれいな答えになると、あることを連想させます。
同じように積分でしか説明できない「●●錐(すい)」の体積です。
小学生のときやりましたよね。「錐の体積=底面積×高さ×1/3」
なんじゃこの1/3倍ってのは!というやつ。
実はこれ、先ほどの積分の考え方から導かれた公式なんです。
ただし小中学生には厳密には説明できないので、苦肉の策として唯一説明できる立方体の例を出したりします。
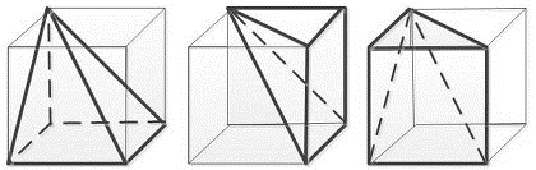
ホラ、同じ四角錐を3つ集めたら立方体(四角柱)になるだろ?
だから錐1つ分の体積は、柱の1/3なのさ! という感じです。
まあ、この方法だと「円錐の場合は?」って訊かれたらアウトですが。
でもさすがに積分は高3ぐらいまで勉強していかないと理解できないですから、「立体を薄くスライスして体積を足していく積分という方法で式を作ったんだよ」という概念だけわかってもらうしかありません。
さて今回の爪形、きれいな答えになるということは、錐の体積のときと同様に小学生でも求められる公式を作ることができるのではないか?
ということで、積分の概念を利用して作ってみた公式は、
ジャジャーン!爪形の体積=半径×半径×高さ×2/3
ん~、公式を作ったはいいけど、こんな変な立体の公式、必要なのかなあ…。







爪型の体積を計算して見たいのですが、高三の積分で求める方法を教えて下さい(上記で割愛されている部分)
コメントありがとうございます。図を使用しておりますので画像で返信いたします。
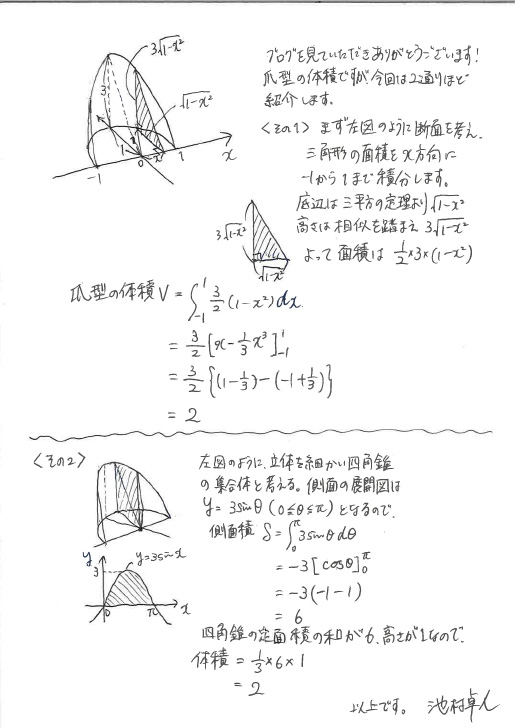
超越数eを絡めた、Πの立体形は、
底面πで高さ(e-1)の『釣り鐘体』に生りそうだ。
『数学妖怪キャラクター』たちの語る自然数は、
[絵本]「もろはのつるぎ]で・・・