私が考える‘ミス’と呼べるものは次の２つしかありません。

1. 九九や足し算・引き算のミス
2. 計算過程での‘写し間違い’

つまり、油断しなければ絶対に間違えなかったはずのものです。
その類のミスばかりであれば、「正解したい」という気持ちのもと丁寧に臨めば問題ありません。

それ以外の間違え方をした場合、次のような可能性があります。

ア　計算の仕組みを完全には理解していない
イ　わざわざ上記1.　2.を誘発するようなやり方をしている
ウ　訓練不足のため、時間内に終わらず慌てて間違える

まぁ、大抵の場合はア～ウが複合し、その結果1.　2.まで引き起こして惨敗…という状態になっているはずです。
というわけなので、単に「計算練習をもっとやりなさい」という指示をしたこところでザルに水を入れるだけの結果になりますので、‘ミスの内容’を見てあげたいところです。
では、上記について詳しく説明します。

ア　計算の仕組みを理解すべし

「計算は機械作業。だからガンガン量をこなして慣れればいいのよ」なんてお子さんをあおったりしてはダメです。もちろん、計算には機械作業的な側面はあります。
しかし、それは理屈を理解してからの話です。例えばこういうのはどうでしょう。

例題
を計算しなさい。

これは中１の夏ぐらいに扱う計算ですが、習いたてだと次のような間違いが多く見られます。

　まずは通分して…

　よし、引き算だ。

　はい、出来上がり。え？間違えてるの？

という感じです。
現場で見ている私たちからすると「あるある」的なオーソドックスな間違え方です。
分数の前についている符号がマイナスのときは要注意です。
この符号は「分数全体についている」ということを意識すれば、

　←分子全体に－の符号がついているので（　）をつける。

　慎重に（　）を外して…

　これで正解です。

このような理解不足による間違いは、なかなか自分で修正できるものではありません。ある程度、誰かが見つけて指摘してあげなければ難しいでしょう。

イ　ミスを生みやすい＝工夫が足りない

よく小学生がこんな計算を正面からまともにやっているのを見ます。

これは大変です。25×3.14を筆算して、それをまた筆算で2で割る。
こんなことをあと２回も繰り返して、最後にさらに筆算で引き算を２回。

こんな長い旅路であれば、道中に九九や引き算のミスぐらい出そうなものです。
ちなみにこの例題では、次のようにやるとよいでしょう。

5×5×3.14÷2-3×3×3.14÷2-2×2×3.14÷2　ひとまず3.14以外の部分を先に。
＝12.5×3.14-4.5×3.14-2×3.14　←ここで、よくある工夫を。
＝（12.5-4.5-2）×3.14
＝6×3.14
＝18.84

最後のかけ算以外の部分は暗算レベルでできますから、実質的に面倒な筆算は最後だけです。
手間も時間もかかりませんから、圧倒的に間違いにくいはずです。
とはいえ、中学以降の数学になれば、この手の問題では円周率が「π」になりますから、必然的に上のような流れで計算することになりますが。

この場合の工夫については、「そうやった方がいいよ」と声をかけても、子どもたちはすぐにそうするようになるわけではありません。
なぜなら、その工夫を‘ありがたい’と思っていなかったり、工夫に気づくやり方をしていなかったりするからです。

前者の場合には上記のような面倒なものをやらせることで、工夫のありがたさに気づかせればよいのですが、後者の場合にはもしかしたら式を‘分断’しているのかもしれません。

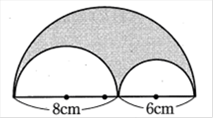
図の斜線部の面積を求める問題があったとします。
このときの計算がまさに先ほどの式になるのですが、部分をそれぞれ計算する子どもが多いために工夫に気づきません。

すなわち「5×5×3.14÷2」だけをひとまず計算してしまうのです。
のちに出てくる同じような計算については考えもしないためでしょう。
だから、先を見通す力も必要になってきます。

最後の答えにたどり着くまでに一通りのことを考えて、一本の式にしてしまうこと。
これはとても重要です。
中学高校以降の数学においてもそれは同じです。皆さんも、「あ、一本の式にしておけば約分で全部消えてたのか…」なんていう経験があると思います。

そういう部分も含めて、子どもに「ああ、それはかなり便利だな。次からはそうしよう」と心から思わせるような、‘大人側の工夫’が必要なのです。

ウ　訓練の不足から起こること

ほとんど言うべきことは言ってしまいましたが、最後に一つ。
工夫をする柔軟な思考があって時間短縮ができれば、制限時間に追われてミスをすることも減ってきます。

しかしながら、練習量が足りなければ‘いちいち工夫を考えてしまう’ということになります。
要は単なる計算なのだから（もちろん仕組みを理解している前提で）、最終的には機械的に正確に答えが出せればよいわけです。
そこに変な労力をかけるのでなく、本編の思考力を問う設問にじっくり時間をかけたいところですよね。

だから、「この手順で書く」「ここではこういう工夫をする」という基本的ないくつかのパターンは反射的に出てくるぐらいの訓練は必要だということです。

ということで、長々と書きましたが、計算一つとってみても「習うより慣れろでガリガリやれ」の一言ではなかなか変わらないということはご承知おきいただきたいかなと。