問い
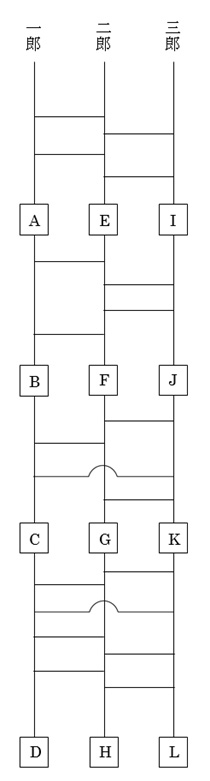
下のようなアミダくじがあります。ただし、ちょっと特殊なアミダで、ゴールも含めて途中にそれぞれ４ヶ所のチェックポイントがあります。各チェックポイントでは、通過した人に応じて得点が与えられます。一郎が通過した場合は1点、二郎が通過した場合は2点、三郎が通過した場合は3点が、そのチェックポイントの得点になります。例えば、一郎はスタート地点からE→F→C→Lの順でチェックポイントを通過するので、これら４つのチェックポイントにはそれぞれ1点が与えられます。最終的には縦に並んだチェックポイントに与えられた得点を合計します。アミダをやってみればわかりますが、A,B,C,Dに与えられた得点の合計は10点、E,F,G,Hに与えられた得点の合計は6点、I,J,K,Lに与えられた得点の合計は8点となります。では問題です。これら縦に並んだチェックポイントの得点の和を全て等しくするためには、このアミダのどこに線を描き加えればよいでしょうか。できれば、なるべく少ない本数で考えてみて下さい。